The discussion of algorithms continues with Insertion Sort, the third overall and the second sorting algorithm covered after starting off with bubble sort. Much like bubble sort and selection sort, insertion sort is a simple, easy to understand sorting algorithm that requires very little code to implement. Keep reading to learn how it works and follow along with a code example of how to implement it as well as a discussion of when it might be the ideal sorting algorithm to use in your own code.
Introduction
Insertion sort works by building the end result (typically an array or list of some kind) one item at a time by comparing the value the data structure will be sorted by. Just as with other simple sorting algorithms, it’s not particularly efficient with a large set of values, but does shine in certain optimal scenarios, which we will cover later.
For a visual demonstration of insertion sort, here’s a quick graphic to help with the concept
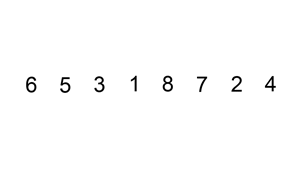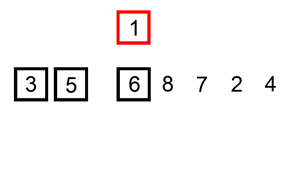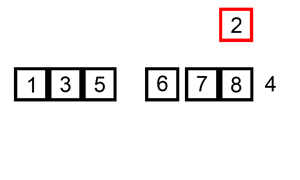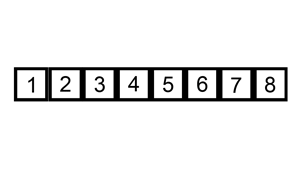
As you can see from the graphic above, insertion sort iterates over the list, from beginning to end, shifting certain portions of the sorted list depending on where the current value needs to be inserted at. These iterations continue until the end of the list is reached and all sorting has completed. For each item that gets removed to be inserted somewhere else, the already sorted portion of the list is checked from largest value to smallest, to determine which position the removed item should be inserted at.
The Code (JavaScript)
Let’s start off by composing our method signature and the beginning of the function, and then we’ll prepare some tests. We will start our outer loop with our position variable i at 1, not 0. This is because the first element will get sorted automatically as we start making our comparisons and sorting the list items. We will continue comparing the list items until we reach the end of the array, so our while loop condition is i < unsortedArray.length .
1
2
3
4
5
6
7
const InsertionSort = (unsortedArray) => {
let i = 1;
while(i < unsortedArray.length) {
}
};
Tests
We don’t need a particularly large number of tests for the purposes of testing this code. I’m going to go with three tests:
- Sequential numbers out of order
- Sequential numbers out of order that contain negative numbers
- Non-sequential numbers out of order that contain duplicate values
Here’s the code for ours tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// unit tests
// Sequential numbers out of order
const array1 = [5,2,7,4,3,1,6];
InsertionSort(array1);
console.log(array1); // [1,2,3,4,5,6,7]
// Sequential numbers out of order that contain negative numbers
const array2 = [-1,-2,4,0,3,5,2,1];
InsertionSort(array2);
console.log(array2); // [-2,-1,0,1,2,3,4,5]
// Non-sequential numbers out of order that contain duplicate values
const array3 = [61,25,10,55,49,32,70,61];
InsertionSort(array3);
console.log(array3); // [10,25,32,49,55,61,61,70]
After I’ve completed all of the posts about sorting algorithms, I think I’ll revisit them with a post where we performance test them all against each other and find the sweet spot where each one performs best.
Back to the code
Now that we have our tests ready, it’s time to complete writing the function. We left off after defining the outer loop of the function where we keep iterating until we’ve reached the end of the items. Next, we need to define an inner loop (so this is a nested while loop scenario). I’ll add comments to the code block here explaining what everything is doing and why.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const InsertionSort = (unsortedArray) => {
let i = 1;
while(i < unsortedArray.length) {
// start the inner loop (j) beginning at the first position where the item
// at that position needs to be compared to the item in the position before it
let j = i;
// keep looping as long as we are not at the first position (j > 0)
// and as long as the item before position j is greater than the item at
// position j
while(j > 0 && unsortedArray[j - 1] > unsortedArray[j]) {
// swap the items at positions j and j - 1
let temp = unsortedArray[j];
unsortedArray[j] = unsortedArray[j - 1];
unsortedArray[j - 1] = temp;
// decrease j by 1 in case we need to continue moving the item swapped
// to the left further to the left because we haven't encountered a value
// that's less than that item yet.
--j;
}
// increase the position to move to the next position in the list
i++;
}
};
As it stands now, the function above will work, and all the tests will pass. However, it’s not as optimal as it could be. Can you tell what could be improved to make this algorithm more efficient? If you step through the code and examine the results after some iterations of the loops, here’s what you would see.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// Here's the first test case, and the array we start with looks like this
[5,2,7,4,3,1,6]
// After the first iteration, the array becomes this, moving 2 in front of 5
[2,5,7,4,3,1,6]
// After the second iteration, the array is still the same as above, because 7 is
// greater than 5 so no items need to be moved
[2,5,7,4,3,1,6]
// After the third iteration, the array looks like this, with 4 placed in front of 7
[2,5,4,7,3,1,6]
// But what we really want here, is for 4 to have been placed in front of 5.
// That *will* happen, but not until the next iteration. How can we modify this code
// so that after the third iteration our array would look like this?
[2,4,5,7,3,1,6]
As you can see, we have a slight inefficiency we can work out of our code. If you’d like to challenge yourself, before reading any further, take the function code above and try to optimize it so that any items being shifted to the left get swapped in one assignment, rather than one position at a time. Hint: the inner loop would only perform one assignment each time.
The Slightly Improved Version
In order to move the current value into the correct position in one assignment, here’s what we can do. The outer loop stays the same, with the initialization of i to 1, and the outer while loop condition beingi < unsortedArray[i] . However, once inside the outer loop, that’s where things change a bit. I’ll provide code comments to explain below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const InsertionSort = (unsortedArray) => {
let i = 1;
while(i < unsortedArray.length) {
// initialize and set temp value outside of the inner loop instead of inside
let temp = unsortedArray[i];
// initialize j to i - 1, instead of i
let j = i - 1;
// the inner while loop condition changes from j > 0 to j >= 0 and from
// unsortedArray[j - 1] > unsortedArray[j]) to
// unsortedArray[j] > temp
while(j >= 0 && unsortedArray[j] > temp) {
// inside the loop the only swap we perform is to move values
// to the right (forward in the array) and decrement the j position
unsortedArray[j + 1] = unsortedArray[j];
--j;
}
// perform the assignment one time here, after execution exits the inner loop
unsortedArray[j + 1] = temp;
i++;
}
};
You might be wondering why I’m saying this version is improved. To be completely clear, it is a minor improvement, but still an improvement. In the improved version the inner loop (which executes many more times than the outer loop) only makes one assignment each time, swapping the value at j + 1 with j, which just shifts the values to the right or “upwards” making room for the temp value to be assigned after the inner loop finishes. The first version of the function on the other hand performed 3 assignments with every execution of the inner loop.
Recursive Version
There’s also a way to write this function utilizing recursion where the recursion basically replaces the outer loop. I will leave it as a challenge to you to see if you can figure it out, but if you want to just view the code, I’ve placed a copy of it in my GitHub Algorithms repo. Just look here.
Wrapping Up
The last thing that might be helpful to understand about insertion sort is, when should you use it? After all, there are general purpose sorting algorithms that are faster, such as merge sort and quick sort. A good rule of thumb on when to use insertion sort is when the list to be sorted contains somewhere between 5 and 50 items. Since the actual performance of sorting algorithms can vary by execution environment and implementation, you might want to benchmark your code to truly see where you get the best performance.
That wraps it up for insertion sort. In future posts, we will discuss other sorting algorithms such as quick sort and merge sort. I’ll come back here and link those posts once I’ve posted them. Stay tuned!
